CollDet - A Library for Collision Detection

Collision Detection Pipeline

Slides

Features

• Boxtree and Dop-Tree for the narrow-phase
• Grid for accelerating the broad-phase
• Convex hull pre-checks (not based on i_collide)
• Supports polygon soups
• The whole pipeline is implemented
• You can define your own collision callback classes
• Support for multi-threading
• Easy-to-use interface
• Runs on Linux, Mac, and Windows

Prerequisites

• OpenSG Version 1.2 or higher
• gcc 3.5 or higher, Visual Studio 2003 or higher, or Intel compiler 8.0

Download

Here is the documentation (generated using doxygen) as individual HTML pages, as a PDF, and as a ZIP archive.

Note that there is a copyright / license that basically says: you can use it for free for academic purposes, but if you want to use it for commercial or other non-academic purposes, then we must negotiate some royalty (which could be a hardware donation, money, etc.). If you are interested, please send me an email.

Benchmarking Results

Publications

• The BoxTree: Exact and Fast Collision Detection of Arbitrary Polyhedra, SIVE95 (First Workshop on Simulation and Interaction in Virtual Environments), University of Iowa, July 1995.
• Real-time and Exact Collision Detection for Interactive Virtual Prototyping, Proc. of the 1997 ASME Design Engineering Technical Conferences, September 14-17, 1997, Sacramento, California. Paper # CIE-4306.
• Rapid Collision Detection by Dynamically Aligned DOP-Trees, Proc. of IEEE Virtual Reality Annual International Symposium; VRAIS '98. Atlanta, Georgia; March 1998. Pages 90-97.
• Optimizing the Collision Detection Pipeline, Proc. of the First International Game Technology Conference (GTEC), Hong Kong, 18-21 January 2001.
• A Benchmarking Suite for Static Collision Detection Algorithms, International Conference in Central Europe on Computer Graphics, Visualization and Computer Vision (WSCG), January 29 - February 1, 2007.
  For further information please visit also our project homepage.
• More publications can be found on our list of publications.

Screenshots

Intersection

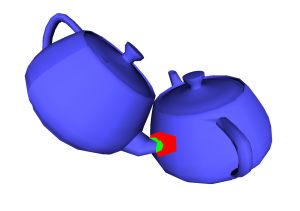On the left side you can see the intersecting triangles. Click on the image to see a small video.

Doptree

Discrete orientation polytopes (DOPs) are convex polytopes whose faces can have only normals which come from a fixed small set of orientations (k-DOPs). In order to be able to apply an interval test to DOPs, one restrict the set of orientations further such that for each orientation of the set there is also an anti-parallel one. Thus, this special kind of k-DOPs can be viewed as a generalization of axis-aligned boxes. We have determined 24 as the optimal number of orientation. (For further information: Rapid Collision Detection by Dynamically Aligned DOP-Trees) The animation on the right shows the first 10 DOP-Tree levels.

Boxtree

These axis-aligned bounding volumes are called Box Tree. Of course, when objects move, they are no longer aligned with respect to the world s coordinate frame. So, when using this type of BVs, the task is to devise algorithms for efficient overlap tests of tumbled bounding boxes. Octrees are a special case of BoxTrees. However, BoxTrees allow for finer control on the balancedness. Each node in the BoxTree stores only: the name a of the splitting axis, two positions, two pointers (to the left and right sub-box), and, for leaves only, a pointer to the polygon(s) associated to the leaf. (For further information: Virtual Reality in Assembly Simulation - Collision Detection, Simulation Algorithms, and Interaction Techniques ) The animation on the right shows some level of the boxtree.

Robustness

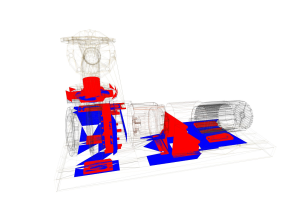Some scenarios for collision detection algorithms include very specific configurations. For example, data gathered from CAD programs contain numerous intersections between coplanar triangles. Therefore, the robustness of the triangle intersection test, but also the numerical stability of the bounding volume tests play an important role for a proper collision response.

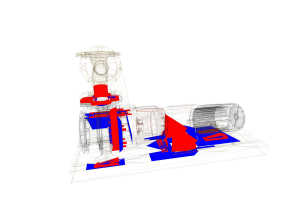The pictures on the left side shows a snapshot from a CAD generated scene. The upper left picture shows the intersecting triangles found by CollDet, the lower left picture those triangles found by another collision detection library. As you can see, CollDet finds 50% more intersecting triangle pairs than the other library. Tests have shown, that many other libraries miss most of the intersecting coplanar triangles. Click here to see a video of the complete scene.

Separating Planes

The separating plane algorithm just needs the set of vertices of the convex hull and its adjacency map. It is based on the following notion: Two objects do not intersect iff there is a plane such that all vertices of the objectes are on different sides. Such a plane is called separating plane The animation on the right shows the line between the closest vertices.